푸앵카레 추측
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
푸앵카레 추측은 3차원 다양체의 위상적 성질에 대한 문제로, 1904년 앙리 푸앵카레가 제기했다. 이 추측은 기본군이 자명한 3차원 다양체가 3차원 구와 위상동형인지 묻는 질문으로, 20세기 초 많은 수학자들이 증명을 시도했으나 난항을 겪었다. 2002년 그리고리 페렐만이 리치 흐름과 수술 기법을 활용하여 푸앵카레 추측과 서스턴의 기하화 추측을 증명했고, 2006년 그의 증명이 옳다는 결론이 내려졌다. 페렐만은 이 업적으로 필즈상과 밀레니엄 상을 받았지만, 수상을 거부했다. 푸앵카레 추측은 3차원 공간의 위상적 성질에 관한 것이며, 4차원 시공간 다양체인 우주의 모양과는 직접적인 관련이 없다.
더 읽어볼만한 페이지
- 3-다양체 - 기하화 추측
기하화 추측은 콤팩트 연결 소 3차원 유향 다양체를 8가지 서스턴 기하 중 하나의 기하 구조를 갖는 조각들로 분해할 수 있다는 내용의 3차원 다양체 분류 프로그램으로, 푸앵카레 추측의 일반화이며 2003년 그리고리 페렐만에 의해 증명되었다. - 3-다양체 - 라이데마이스터 비틀림
라이데마이스터 비틀림은 콤팩트 리만 다양체와 벡터 다발에 대한 불변량으로, 해석적 정의와 위상수학적 정의가 있으며, 치거-뮐러 정리에 의해 두 정의가 일치하고, 천-사이먼스 이론의 섭동 이론적 양자화에 응용된다. - 밀레니엄 문제 - P-NP 문제
P-NP 문제는 계산 복잡도 이론에서 P와 NP 복잡도 종류의 관계에 대한 미해결 문제로, 컴퓨터 과학과 수학에 혁명적인 변화를 가져올 것으로 예상되며 암호학, 최적화, 인공지능 등 다양한 분야에 큰 영향을 미칠 수 있다. - 밀레니엄 문제 - 리만 가설
리만 가설은 리만 제타 함수의 자명하지 않은 모든 영점의 실수부가 1/2이라는 추측으로, 힐베르트 문제와 클레이 수학 연구소의 밀레니엄 문제 중 하나이며 정수론과 복소해석학을 연결하는 다양한 수학적 명제들과 동치이다. - 기하학적 위상수학 - 클라인 병
클라인 병은 펠릭스 클라인이 발견한 비가향적인 2차원 다양체로, 3차원 공간에서는 자기 교차 없이 존재할 수 없으며 한쪽 면만 가지는 닫힌 곡면이다. - 기하학적 위상수학 - 기하화 추측
기하화 추측은 콤팩트 연결 소 3차원 유향 다양체를 8가지 서스턴 기하 중 하나의 기하 구조를 갖는 조각들로 분해할 수 있다는 내용의 3차원 다양체 분류 프로그램으로, 푸앵카레 추측의 일반화이며 2003년 그리고리 페렐만에 의해 증명되었다.
| 푸앵카레 추측 |
|---|
2. 역사
1904년 앙리 푸앵카레가 3차원 다양체의 위상적 성질에 대한 질문을 제기하면서 푸앵카레 추측의 역사가 시작되었다.[52] 푸앵카레는 호몰로지 군이 자명한 3차원 다양체가 3차원 구와 위상동형인지에 대한 질문을 던졌으나, 이후 푸앵카레 호몰로지 구라는 반례를 발견하고 기본군을 사용하여 질문을 수정하였다.[17][13]
20세기 초, 여러 수학자들이 푸앵카레 추측에 도전했지만 증명에 어려움을 겪었다. J. H. C. 화이트헤드는 증명을 주장했지만 후에 철회하기도 했다. 1950년대와 1960년대에도 여러 수학자들이 증명을 시도했지만 결함이 발견되었다.
5차원 이상인 경우는 스티븐 스메일이, 4차원의 경우는 마이클 프리드먼이 증명하여 각각 1966년과 1986년에 필즈상을 수상하였다.[70][71][72] 이로써 원래의 3차원 푸앵카레 추측만이 남게 되었다.
1982년 리처드 S. 해밀턴은 리치 흐름을 도입하여 푸앵카레 추측의 특수한 경우를 증명하는 방법을 제시했다. 이후 그리고리 페렐만은 리치 흐름을 기반으로 한 증명을 arXiv에 발표하였다.[70][71][72] 국제 수학 연맹(IMU)은 3년간의 분석 끝에 페렐만의 풀이를 인정하고 2006년 필즈상 수상자로 선정했으나, 페렐만은 수상을 거부했다. 같은 업적으로 2010년 밀레니엄상 수상자로도 선정되었으나 이 역시 거부하였다.[73][74]
1800년대에 베른하르트 리만과 엔리코 베티는 다양체의 위상 불변량 연구를 시작했다.[9][10] 푸앵카레는 기본군을 도입하여 베티 수로 완전히 특징지어지지 않는 3차원 다양체의 예시를 제시하고, 기본군이 다양체를 위상적으로 특징짓기에 충분한지 질문했다.[11][12][13]
2. 1. 푸앵카레의 질문
1904년 앙리 푸앵카레는 자신의 논문에서 3차원 다양체의 위상적 성질에 대한 질문을 던졌다.[52] 그는 3차원 구의 호몰로지 군이 자명하다는 점에 주목하여, 역으로 호몰로지 군이 자명한 3차원 다양체가 3차원 구와 위상동형인지 질문했다.위상기하학에서 2차원 구면과 1차원 구면(원주)은 단일 연결이라는 근본적인 특징을 가지고 있는데, 3차원 표면에서도 구에 대해서 그러한 사실이 성립하는지에 대한 것이었다. 구체적으로 어떤 하나의 닫힌 3차원 공간에서 모든 폐곡선이 수축되어서 하나의 점이 될 수 있다면, 이 공간은 반드시 원구로 변형될 수 있다는 것이었다.
이후 푸앵카레는 자신의 질문에 대한 반례(푸앵카레 호몰로지 구)를 발견하고, 호몰로지 군 대신 기본군을 사용하여 질문을 수정했다.[17][13] 즉, 기본군이 자명한 3차원 다양체가 3차원 구와 위상동형인지 질문했다.
> 한 가지 질문이 남아 있다. V의 기본군이 V가 단일 연결되지 않고 항등원으로 축소될 수 있는가? [...] 그러나 이 질문은 우리를 너무 멀리 데려갈 것이다.
이 발언에서 푸앵카레는 "단일 연결"이라는 용어를 현대적 용법과 다르게 사용했다.[12][16] 문맥에서 추론하면,[18] 푸앵카레는 기본군의 자명성이 구를 고유하게 특징짓는지 묻고 있었다.[14]
푸앵카레 추측은 현재 "단일 연결인 3차원 닫힌 다양체는 3차원 구와 위상 동형이다"로 표현된다.[45] 즉, 경계를 갖지 않는연결[53]이고 콤팩트인 3차원 다양체는 임의의 루프를 1점으로 수축할 수 있다면, 3차원 구와 위상 동형이라는 것이다.

2. 2. 초기 증명 시도와 난관
20세기 초, 여러 수학자들이 푸앵카레 추측에 도전했으나, 증명에 어려움을 겪었다. J. H. C. 화이트헤드는 증명을 주장했지만, 후에 철회했다. 그 과정에서 그는 와 위상동형이 아닌 단순 연결(실제로 수축 가능, 즉 점과 호모토피 동치) 비콤팩트 3차원 다양체의 몇 가지 예를 발견했는데, 그 전형적인 예는 현재 화이트헤드 다양체라고 불린다.[14]1950년대와 1960년대에 다른 수학자들도 이 추측의 증명을 시도했지만, 결함을 발견했다. 조르주 드 람, R. H. 빙, 볼프강 하켄, 에드윈 E. 모이즈, 크리스토스 파파키리아코풀로스와 같은 영향력 있는 수학자들이 이 추측을 증명하려고 시도했다. 1958년, R. H. 빙은 푸앵카레 추측의 약한 버전을 증명했다: 만약 콤팩트 3차원 다양체의 모든 단순 폐곡선이 3차원 공 안에 포함된다면, 그 다양체는 3차원 구와 위상동형이다.[20] 빙은 또한 푸앵카레 추측을 증명하려는 시도의 몇 가지 함정을 설명했다.[21]
시간이 지남에 따라 이 추측은 다루기 특히 까다로운 것으로 명성을 얻었다. 존 밀너는 때때로 잘못된 증명의 오류가 "매우 미묘하고 감지하기 어려울 수 있다"고 언급했다.[23] 이 추측에 대한 연구는 3차원 다양체에 대한 이해를 향상시켰다. 이 분야의 전문가들은 종종 증명을 발표하는 것을 꺼렸고, 그러한 발표를 회의적으로 보는 경향이 있었다. 1980년대와 1990년대에는 몇 가지 널리 알려진 잘못된 증명(실제로 동료 심사 형태로 출판되지 않은)이 있었다.[24][25]
2. 3. 고차원에서의 해결
5차원 이상인 경우 미국의 수학자 스티븐 스메일이 증명하여 1966년 필즈상을 수상하였으며, 4차원에 대한 문제는 마이클 프리드먼이 증명하여 1986년 필즈상을 수상하였다.[70][71][72]1961년, 스티븐 스메일은 4차원 이상의 일반화된 푸앵카레 추측을 증명하여 수학자들에게 충격을 주었고, 그의 기법을 확장하여 기본적인 h-코보디즘 정리를 증명했다. 1982년, 마이클 프리드먼은 4차원에서 푸앵카레 추측을 증명했다. 프리드먼의 연구는 4차원 구와 위상 동형이지만 4차원 구와 미분 동형이 아닌 매끄러운 4-다양체의 존재 가능성을 열어두었다. 이른바 4차원에서의 매끄러운 푸앵카레 추측은 미해결 상태로 남아 있으며 매우 어려운 문제로 여겨진다. 밀너의 이국적인 구는 예를 들어 7차원에서 매끄러운 푸앵카레 추측이 거짓임을 보여준다.
n차원 호모토피 구는, n차원 구와 호모토피 동치인 n차원 닫힌 다양체를 말한다. 일반적인 위상 공간에서는 호모토피 동치가 위상 동형보다 약한 개념이지만, 그 역이 3차원 구의 경우에는 성립한다는 것이다. 그래서 고차원에서는 "n차원 호모토피 구는 n차원 구와 위상 동형이다." 와 같이 일반화 할 수 있다.
푸앵카레 추측을 n차원으로 일반화하면 n=2 에서의 성립은 고전적인 사실이며, n≥4 의 경우에는 20세기 후반에 증명이 얻어졌다. n≥5 일 때는 스티븐 스메일에 의해, n=4 일 때는 마이클 프리드먼에 의해 증명되었다. 두 사람 모두, 그 업적으로 필즈상을 수상했다. 스메일의 증명은 미분 위상 기하학적인 것이었지만, 프리드먼의 증명은 순수한 위상 기하학적인 것이다. 실제로, 프리드먼의 결과는 그 직후 도널드슨에 의한 이종 4차원 유클리드 공간 (위상적으로는 통상의 4차원 공간이지만, 미분 구조가 다른 것)의 발견으로 이어졌다. 이로써 3차원 푸앵카레 추측만 남기고, 고차원 푸앵카레 추측은 먼저 결론이 났다. ( 미분 동상에 대해서는 4차원 푸앵카레 추측도 미해결이다.)
2. 4. 해밀턴의 프로그램과 페렐만의 증명
1982년 리처드 S. 해밀턴은 리치 흐름을 도입하고 이를 사용하여 푸앵카레 추측의 몇 가지 특수한 경우를 증명하는 방법을 제시했다.[28] 리치 흐름은 다양체의 음의 곡률 부분을 확장하고 양의 곡률 부분을 수축시키는 방식으로 작동한다. 해밀턴은 리만 다양체가 모든 곳에서 양의 리치 곡률을 갖는 경우, 리치 흐름을 통해 리만 계량 가 상수 양의 곡률 중 하나로 부드럽게 수렴한다는 것을 보여주었다. 이는 푸앵카레 추측의 특수한 경우, 즉 콤팩트 단일 연결 3차원 다양체가 양의 리치 곡률의 리만 계량을 지원한다면 3-구와 미분 동형이어야 한다는 것을 증명한 것이다.그러나 임의의 리만 계량만 있는 경우에는 리치 흐름 방정식이 더 복잡한 특이점을 초래한다. 그리고리 페렐만은 이러한 특이점이 유한 시간 내에 나타난다면 수축하는 구 또는 원통처럼 보일 수밖에 없다는 것을 보여주었다. 그는 특이점을 따라 다양체를 잘라 여러 조각으로 나눈 다음, 각 조각에서 리치 흐름을 계속 진행하는 '수술을 동반한 리치 흐름' 절차를 고안했다.
페렐만은 곡선 축소 흐름을 기반으로 하는 별도의 논증을 통해, 단일 연결 콤팩트 3차원 다양체에서 수술을 동반한 리치 흐름의 모든 해가 유한 시간 내에 소멸한다는 것을 증명했다. 토비아스 콜딩과 윌리엄 미니코지는 최소 곡면의 최소-최대 이론과 기하 측정 이론을 기반으로 하는 대안적인 논증을 제공했다.
2002년 말과 2003년에 페렐만은 arXiv에 세 편의 논문을 게시했다.[29][30][31] 이 논문들에서 그는 리처드 S. 해밀턴이 이전에 개략적으로 설명한 리치 흐름 프로그램을 완성하여 푸앵카레 추측과 서스턴의 기하화 추측의 증명을 스케치했다.
2006년 5월부터 7월까지 여러 연구 그룹이 페렐만의 증명을 검증하고 세부 사항을 채운 논문을 발표했다.
- 브루스 클라이너와 존 W. 로트는 기하화 추측에 대한 페렐만의 증명 세부 사항을 채운 논문을 발표했다.[32]
- 차오 화이동과 주 시핑은 푸앵카레 및 기하화 추측의 완전한 증명을 설명하는 논문을 발표했다.[33]
- 존 모건과 강 티안은 푸앵카레 추측의 자세한 증명을 제공하는 논문을 발표했다.[35]
세 그룹 모두 페렐만의 논문의 틈새가 사소하며 그의 기술을 사용하여 채울 수 있음을 발견했다. 2006년 12월, 저널 ''사이언스''는 푸앵카레 추측의 증명을 올해의 획기적인 발견으로 선정했다.[5]
3. 증명의 핵심 아이디어: 리치 흐름과 수술
페렐만의 증명은 해밀턴이 제시한 리치 흐름과 수술(surgery)이라는 두 가지 핵심 아이디어를 기반으로 한다. 해밀턴은 리치 흐름을 사용하여 푸앵카레 추측의 특수한 경우를 증명하는 방법을 보였으나, 일반적인 경우에는 특이점 문제로 인해 어려움을 겪었다. 페렐만은 해밀턴의 연구를 확장하여 리치 흐름과 수술을 결합한 새로운 방법을 제시하고, 이를 통해 푸앵카레 추측을 증명했다.
페렐만은 먼저 미지의 단일 연결 닫힌 3차원 다양체에 리만 계량을 부여하고, "리치 흐름 방정식"을 사용하여 계량을 개선하려 했다. 리치 흐름은 다양체의 음의 곡률 부분을 확장하고 양의 곡률 부분을 수축시켜 다양체를 더 둥근 모양으로 변형시킨다. 그러나 이 과정에서 특이점이 발생할 수 있는데, 페렐만은 이러한 특이점이 유한 시간 내에 나타난다면 수축하는 구 또는 원통처럼 보일 수밖에 없다는 것을 보였다.
페렐만은 특이점이 발생하는 지점에서 다양체를 잘라내고, 잘라낸 부분에 캡을 씌워 다시 리치 흐름을 진행하는 "수술"이라는 절차를 도입했다. 그는 곡선 축소 흐름을 기반으로 하는 논증을 통해, 수술을 동반한 리치 흐름의 모든 해가 유한 시간 내에 소멸한다는 것을 보였다.[45][60][61]
3. 1. 리치 흐름
리처드 S. 해밀턴은 다양체에 리치 흐름을 도입하고 이를 사용하여 푸앵카레 추측의 몇 가지 특수한 경우를 증명하는 방법을 제시하였다.[28] 리치 흐름은 다양체의 음의 곡률 부분을 확장하고 양의 곡률 부분을 수축시킨다.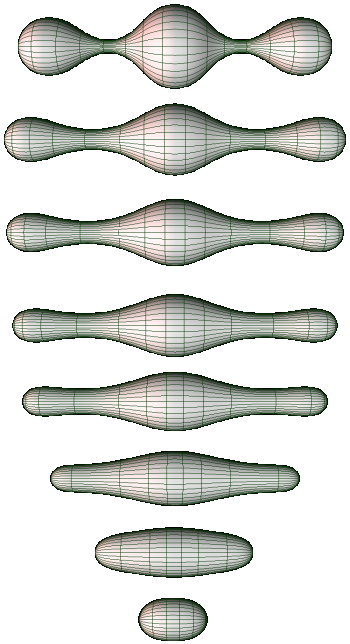
리치 흐름 방정식은 다음과 같다.
:
여기서 ''g''는 계량이고 ''R''은 그 리치 곡률이며, 시간 ''t''가 증가함에 따라 다양체를 이해하기 쉬워지기를 바란다.
어떤 경우에는 리만 다양체가 모든 곳에서 양의 리치 곡률을 갖는 경우, 매개변수 값의 유계 구간 ()에 대해서만 따를 수 있으며, 숫자 가 존재하여 로 갈 때 리만 계량 가 상수 양의 곡률 중 하나로 부드럽게 수렴한다. 상수 양의 곡률의 리만 계량을 지원할 수 있는 유일한 단일 연결 콤팩트 다양체는 구이므로, 콤팩트 단일 연결 3차원 다양체가 양의 리치 곡률의 리만 계량을 지원한다면 3-구와 미분 동형이다.
임의의 리만 계량만 있는 경우, 리치 흐름 방정식은 더 복잡한 특이점을 초래해야 한다. 그리고리 페렐만은, 특정 관점에서 볼 때, 이러한 특이점이 유한 시간 내에 나타난다면, 수축하는 구 또는 원통처럼 보일 수밖에 없다는 것을 보여주었다. 이 현상에 대한 정량적인 이해를 통해, 그는 특이점을 따라 다양체를 잘라 다양체를 여러 조각으로 나눈 다음, 이러한 각 조각에서 리치 흐름을 계속 진행한다. 이 절차를 수술을 동반한 리치 흐름이라고 한다.
페렐만은 열 방정식과 유사하게 동작하는 리치 흐름을 사용하여 다양체를 변형함으로써 추측을 증명했다. 열 방정식은 물체 전체로 열이 확산되는 것을 설명한다. 리치 흐름은 일반적으로 다양체를 더 둥근 모양으로 변형시키지만, 수학적 특이점이라고 알려진 일부 경우에서는 다양체를 자체로부터 멀어지게 늘린다. 페렐만과 해밀턴은 특이점에서 다양체를 잘라내어("수술"이라고 함) 분리된 조각들이 공 모양을 형성하도록 했다.
3. 2. 수술
해밀턴은 리치 흐름 방정식에서 발생하는 특이점을 해결하기 위해 수술(Surgery)이라는 방법을 고안했다. 페렐만은 이 방법을 발전시켜 푸앵카레 추측을 증명하는데 활용했다.수술은 리치 흐름 과정에서 발생하는 특이점을 제거하는 기법이다. 특이점이 나타나기 직전, 다양체의 특이점 근처에서 얇은 원통 모양 부분을 잘라낸다. 그 후, 잘라낸 부분의 단면()에 구면 모양의 캡을 씌워 표준적인 모양(구 또는 원기둥)으로 만든다.[45][60] 이 과정을 통해 리치 흐름은 유한한 시간 내에 특이점을 넘어 계속 진행될 수 있게 된다.[45][61]
페렐만은 이러한 수술 과정을 통해 3차원 리치 흐름이 유한한 시간 안에 특이점을 넘어 표준적으로 연장될 수 있음을 증명했다.[45][61]
3. 3. 증명의 개요
그리고리 페렐만은 리치 흐름을 사용하여 다양체를 변형하고, 발생하는 특이점에 '수술'을 적용하여 다양체를 단순한 형태로 만들었다. 그는 열 방정식과 유사하게 작동하는 리치 흐름을 통해 다양체를 변형시켰는데, 이는 일반적으로 다양체를 더 둥근 모양으로 만들지만, 특이점이 발생하면 다양체를 자체로부터 멀어지게 늘린다.[44] 페렐만과 해밀턴은 특이점에서 다양체를 잘라내어("수술"이라고 함) 분리된 조각들이 공 모양을 형성하도록 했다.페렐만은 곡선 축소 흐름을 기반으로 하는 별도의 논증을 제공하여, 수술을 유한 번만 적용해도 충분하며, 최종적으로 다양체가 3차원 구와 위상동형임을 증명했다. 토비아스 콜딩과 윌리엄 미니코지는 최소 곡면의 최소-최대 이론과 기하 측정 이론을 기반으로 하는 대안적인 논증을 제공했다.
증명의 주요 단계는 다음과 같다:
| 단계 | 설명 |
|---|---|
| 1 | 리치 흐름을 사용하여 다양체가 어떻게 변형되는지 보여준다. |
| 2 | 어떤 종류의 특이점이 발생하는지 조사한다. |
| 3 | 수술 과정을 완료할 수 있는지 확인한다. |
| 4 | 수술을 무한히 반복할 필요가 없음을 확립한다. |
페렐만은 특이점이 모두 매우 단순하며, 본질적으로 원통을 다른 차원의 선을 따라 늘여서 만든 형태와 같다는 것을 발견했다. 그는 "감소된 부피"라는 개념을 사용하여 이를 증명했는데, 이는 특정 타원형 연산자의 고유값과 밀접한 관련이 있다.
페렐만은 다양체가 리치 흐름에 의해 변형됨에 따라 고유값이 올라간다는 것을 증명했다. 이를 통해 해밀턴을 걱정하게 했던 몇 가지 특이점을 제거할 수 있었다. 그는 형성되는 모든 가닥을 자르고 캡을 씌울 수 있으며, 한쪽 면에만 튀어나온 것은 없음을 보여주었다.
마지막으로, 페렐만은 경계가 없는 임의의 콤팩트하고 단일 연결된 3차원 다양체를 가져와 리치 흐름을 시작하여 다양체를 둥근 조각으로 변형시킨다. 가닥을 잘라내고 다양체를 계속 변형시켜 결국 둥근 3차원 구의 모음이 남도록 한다. 그런 다음, 그는 구들을 3차원 원통으로 연결하여 원래 다양체를 재구성하고, 이들을 둥근 모양으로 변형시킨 다음, 다양체가 실제로 구와 위상 동형임을 확인한다.
무한히 많은 절단이 필요하지 않다는 것을 증명하기 위해 페렐만은 극소 곡면을 사용했다. 그는 다양체가 잘렸을 때 극소 곡면의 면적이 감소하며, 결국 면적이 너무 작아져서 더 복잡한 조각이 아닌 3차원 구만 잘라낼 수 있음을 증명했다.
4. 기하화 추측과의 관계
윌리엄 서스턴이 제창한 기하화 추측은 3차원 닫힌 다양체의 분류에 대한 것으로, 3차원 푸앵카레 추측을 함의한다.[55] 서스턴의 기하화 추측은 임의의 소(素) 3차원 다양체가 몇 개의 비압축 토러스에 의해 기하 구조를 가진 조각(폐영역)으로 분해된다는 것이며,[58] 기하 구조를 가진 3차원 다양체의 모델은 8개이다.[45]
그리고리 페렐만은 특이점이 발생하는 3차원 다양체에 대하여, 3차원 수술이 있는 리치 흐름(Ricci flow with surgery)을 적용함으로써 기하화 추측을 해결했다.[59]
5. 페렐만의 업적과 수상 거부
2002년 러시아의 수학자 그리고리 페렐만이 arXiv에 푸앵카레 추측의 해법이 포함된 논문을 발표하였다.[70][71][72] 국제 수학 연맹(IMU)은 3년간의 분석 끝에 페렐만의 풀이를 인정하여 2006년 필즈상 수상자로 선정하였으나, 페렐만은 수상을 거부하였다. 같은 업적으로 2010년 3월 18일 밀레니엄상 수상자로도 선정되었으나[73], 이 역시 거부하였다.[74]
2002년부터 2003년에 걸쳐 당시 스테클로프 수학 연구소에 근무하던 페렐만은 푸앵카레 추측을 증명했다고 주장하며, 2002년 11월 11일에 논문을 프리프린트 서버arXiv에 공개했다. 그는 리처드 스트레이트 해밀턴이 창시한 리치 플로우 이론에 "수술"이라고 부르는 새로운 기법을 더하여 확장하고, 서스턴의 기하화 추측을 해결하여 푸앵카레 추측을 해결했다고 선언했다.
페렐만의 증명은 리처드 S. 해밀턴이 개발한 리치 흐름 프로그램을 변형한 버전을 사용한다. 2006년 8월, 페렐만은 리치 흐름에 대한 업적으로 필즈상(15000CAD)을 받았지만 거절했다. 2010년 3월 18일, 클레이 수학 연구소는 페렐만의 증명을 인정하여 100만달러의 밀레니엄 상을 수여했지만, 이 상 또한 거절했다.[41][42][7][43]
2006년 8월 22일, 스페인의 마드리드에서 열린 국제 수학자 대회 개회식에서 페렐만에게 필즈상이 수여되었으나, 페렐만은 이에 참석하지 않고 수상을 거부했다.[63]
2010년 3월 18일, 클레이 수학 연구소는 페렐만에게 밀레니엄 상 수상을 발표했다.[67] 페렐만은 이전에, "수상을 전해들은 후에 생각한다"라고 말했으나, 결국 시상식에는 참석하지 않았다. 연구소의 소장은 "선택을 존중한다"라는 성명을 발표하고, 상금과 상품은 보관된다고 한다.[68]
2010년 7월 1일, 페렐만은 상금 수령을 최종적으로 거절했다고 보도되었다. 거절한 이유는 수학계의 결정에 불공평함이 있다는 것, 푸앵카레 추측 해결에 기여한 리처드 S. 해밀턴에 대한 평가가 충분하지 않다는 점 등을 들었다. 또한, 이 일에 대해 본인은 "이유는 여러 가지가 있다"라고 답했다.[69]
6. 대중적 오해와 진실
푸앵카레 추측은 종종 우주의 모양과 관련지어 설명되지만, 이는 오해이다. 푸앵카레 추측은 "모든 경계가 없는 단일 연결 콤팩트 3차원 다양체는 3차원 구면과 위상동형이다."라는 추측이다.
이는 기하학적 위상수학 분야의 수학적 문제로, 다음과 같이 표현할 수 있다.
>'''푸앵카레 추측'''.3차원 위상 다양체가 닫혀 있고, 연결되어 있으며, 자명한 기본군을 가지면, 3차원 구와 위상동형이다.
원환체와 같은 모양은 비자명한 기본군을 가지며, 표면에 그려진 고리가 점으로 수축될 수 없는 경우가 존재한다. 2차원 구와 원환체는 위상동형이 아니다. 푸앵카레 추측의 2차원 유사체는 1860년대부터 알려진 닫혀 있고 연결된 2차원 위상 다양체의 분류를 통해 참으로 알려져 있다. 그러나 더 높은 차원에서는 닫혀 있고 연결된 위상 다양체는 간단한 분류가 없으므로 푸앵카레 추측을 쉽게 해결할 수 없다.
6. 1. 우주의 모양과의 관계
위상수학의 오랜 난제였던 푸앵카레 추측을 설명하는 많은 교양 매체들을 통해 이 추측이 우주의 대역적 모양을 알아내는 것과 연관이 있다는 설이 대중적으로 퍼져있다.그러나 푸앵카레 추측은 3차원 공간의 위상적 성질에 관한 것이며, 4차원 시공간 다양체인 우주의 모양과는 직접적인 관련이 없다.[52] 이 추측이 제기된 시기는 일반 상대성 이론이 발표되기 이전으로, 우주의 모양에 대한 연구와는 무관하게 제기된 문제이다.
또한, 물리적 우주가 푸앵카레 추측의 조건을 만족하는지(단일 연결, 콤팩트 등)는 알 수 없으며, 관측 가능한 우주 너머의 정보는 얻을 수 없기 때문에 푸앵카레 추측을 통해 우주의 모양을 알아내는 것은 불가능하다.
참조
[1]
서적
Algorithmic Topology and Classification of 3-Manifolds
https://books.google[...]
Springer
[2]
웹사이트
Poincaré, Jules-Henri
http://www.lexico.co[...]
Oxford University Press
[3]
웹사이트
Poincaré
2019-08-09
[4]
웹사이트
Poincaré
2019-08-09
[5]
논문
The Poincaré Conjecture – Proved
2006-12-22
[6]
간행물
Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman
http://www.claymath.[...]
Clay Mathematics Institute
2015-11-13
[7]
웹사이트
Последнее 'нет' доктора Перельмана
http://www.interfax.[...]
2016-04-05
[8]
뉴스
Russian mathematician rejects million prize
http://www.boston.co[...]
2010-07-01
[9]
학위논문
Grundlagen für eine allgemeine Theorie der Functionen
University of Göttingen
[10]
논문
Sopra gli spazi di un numero qualunque di dimensioni
[11]
논문
Sur l'Analysis situs
https://gallica.bnf.[...]
[12]
논문
Analysis situs
http://gallica.bnf.f[...]
[13]
서적
Papers on Topology: Analysis Situs and Its Five Supplements
American Mathematical Society and London Mathematical Society
[14]
서적
Henri Poincaré: A Scientific Biography
Princeton University Press
[15]
논문
Second complément à l'analysis situs
https://zenodo.org/r[...]
[16]
harvtxt
[17]
논문
Cinquième complément à l'analysis situs
https://zenodo.org/r[...]
[18]
harvtxt
[19]
서적
A History of Algebraic and Differential Topology, 1900–1960
Birkhäuser Boston, Inc.
[20]
논문
Necessary and sufficient conditions that a 3-manifold be S3
1958
[21]
학회자료
Some aspects of the topology of 3-manifolds related to the Poincaré conjecture
Wiley
1964
[22]
논문
The Bing–Borsuk and the Busemann conjectures
https://hrcak.srce.h[...]
2008-12-23
[23]
웹사이트
The Poincaré Conjecture 99 Years Later: A Progress Report
http://www.math.suny[...]
2004
[24]
뉴스
What happens when hubris meets nemesis
1987-07
[25]
뉴스
$1 million mathematical mystery "solved"
https://www.newscien[...]
2007-05-05
[26]
서적
Poincaré's Prize: The Hundred-Year Quest to Solve One of Math's Greatest Puzzles
Plume
[27]
문서
Morgan, John W., Recent progress on the Poincaré conjecture and the classification of 3-manifolds.
[28]
논문
Three-manifolds with positive Ricci curvature
1982
[29]
arXiv
The entropy formula for the Ricci flow and its geometric applications
2002
[30]
arXiv
Ricci flow with surgery on three-manifolds
2003
[31]
arXiv
Finite extinction time for the solutions to the Ricci flow on certain three-manifolds
2003
[32]
논문
Notes on Perelman's Papers
[33]
논문
A Complete Proof of the Poincaré and Geometrization Conjectures – application of the Hamilton-Perelman theory of the Ricci flow
http://www.intlpress[...]
2006-06
[34]
arXiv
Hamilton–Perelman's Proof of the Poincaré Conjecture and the Geometrization Conjecture
2006-12-03
[35]
arXiv
Ricci Flow and the Poincaré Conjecture
2006
[36]
서적
Ricci Flow and the Poincaré Conjecture
Clay Mathematics Institute
2007
[37]
논문
Correction to Section 19.2 of Ricci Flow and the Poincare Conjecture
2015
[38]
간행물
Manifold destiny
http://www.newyorker[...]
2006-08-28
[39]
뉴스
Highest Honor in Mathematics Is Refused
https://www.nytimes.[...]
2006-08-22
[40]
문서
A Report on the Poincaré Conjecture. Special lecture by John Morgan.
[41]
웹사이트
Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman
http://www.claymath.[...]
Clay Mathematics Institute
2010-03-18
[42]
웹사이트
Poincaré Conjecture
http://www.claymath.[...]
Clay Mathematics Institute
2018-10-04
[43]
웹사이트
Russian mathematician rejects $1 million prize
https://phys.org/new[...]
Phys.Org
2011-05-15
[44]
서적
The Surprising Resolution of the Poincaré Conjecture. In: Rowe, D., Sauer, T., Walter, S. (eds) Beyond Einstein
Birkhäuser
[45]
서적
Algorithmic Topology and Classification of 3-Manifolds
https://books.google[...]
Springer
[46]
문서
戸田正人 - リッチフローの基礎と三次元多様体の幾何学化
http://www.math.toho[...]
[47]
문서
Eduardo Francisco Rêgo - On the Mechanics of the Poincaré Conjecture an Heuristic Tour.
http://cmup.fc.up.pt[...]
[48]
웹사이트
The Millennium Prize Problems
https://www.claymath[...]
2024-09-10
[49]
문서
「多様体とは何か」(第5章に初心者向け解説有り)小笠英志 ブルーバックス・シリーズ 講談社
https://bookclub.kod[...]
[50]
문서
「ポアンカレ予想」はまだ解けてない!?小笠英志 講談社のweb記事 初心者向け解説
https://gendai.media[...]
[51]
Youtube
天才少女(小1)が4次元微分ポアンカレ予想にアタック開始。 意気込みを語る動画
https://www.youtube.[...]
[52]
웹사이트
Towards the Poincaré Conjecture and the Classification of 3-Manifolds
http://www.ams.org/n[...]
American Mathematical Society
2015-07-18
[53]
문서
多様体が連結であることと弧状連結であることは同値である。
[54]
문서
"#参考文献"
[55]
웹사이트
Geometrization of 3-Manifolds via the Ricci Flow
http://www.ams.org/n[...]
American Mathematical Society
2015-07-18
[56]
문서
小沢誠 - 幾何特論I(3次元多様体)p. 13
http://www.komazawa-[...]
[57]
문서
『100年の難問はなぜ解けたのか 〜天才数学者の光と影〜』NHK出版、2008年6月。pp. 35–60.
[58]
웹사이트
多様体の崩壊-ペレルマンの仕事まで
https://doi.org/10.1[...]
日本数学会
2015-07-17
[59]
문서
本間泰史 - リッチフロー
http://www.f.waseda.[...]
[60]
문서
Lecture
http://www.ams.org/b[...]
[61]
문서
HUAI-DONG CAO , XI-PING ZHU - A COMPLETE PROOF OF THE POINCARE AND GEOMETRIZATION CONJECTURES
http://www.ims.cuhk.[...]
[62]
방송
NHKスペシャル 2007年10月22日放送分 『100年の難問はなぜ解けたのか 〜天才数学者 失踪の謎〜』 より
[63]
웹사이트
Highest Honor in Mathematics Is Refused
https://www.nytimes.[...]
The New York Times
2015-07-09
[64]
웹사이트
難問奇問と天才奇人数学者 〜ポアンカレ予想の解決〜
https://www.itmedia.[...]
2015-07-01
[65]
문서
Breakthrough of the Year
[66]
문서
Manifold Destiny
http://www.newyorker[...]
[67]
웹사이트
Poincaré Conjecture
http://www.claymath.[...]
Clay Mathematics Institute
2015-07-01
[68]
뉴스
数学者ペレルマン、授賞式に姿見せず 懸賞金1億円
http://japanese.ruvr[...]
2015-07-01
[69]
뉴스
変わり者数学者、やっぱり賞金拒否 ポアンカレ予想解決
http://www.asahi.com[...]
2015-07-01
[70]
저널
The entropy formula for the Ricci flow and its geometric applications
2002
[71]
논문
Ricci flow with surgery on three-manifolds
2003
[72]
논문
Finite extinction time for the solutions to the Ricci flow on certain three-manifolds
2003
[73]
웹인용
Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman
http://www.claymath.[...]
2010-04-08
[74]
뉴스
Worlds cleverest man turns down $1million prize
http://www.dailymail[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com